Section: Research Program

High-level HPC libraries and applications

In this research topic, we focus on developing optimized algorithms and software for high-performance scientific computing and image processing.

Taking advantage of heterogeneous parallel architectures

Activity description

In recent years and as observed in the latest trends from the Top 500 list (http://www.top500.org/ ), heterogeneous computing combining manycore systems with accelerators such as Graphics Processing Units (GPU) or Intel Xeon Phi coprocessors has become a de facto standard in high performance computing. At the same time, data movements between memory hierarchies and/or between processors have become a major bottleneck for most numerical algorithms. The main goal of this topic is to investigate new approaches to develop linear algebra algorithms and software for heterogeneous architectures  [42] , [149] , with also the objective of contributing to public domain numerical linear algebra libraries (e.g., MAGMA (Matrix Algebra on GPU and Multicore Architectures, http://icl.cs.utk.edu/magma/ )).

Our activity in the field consists of designing algorithms that minimize the cost of communication and optimize data locality in numerical linear algebra solvers. When combining different architectures, these algorithms should be properly “hybridized”. This means that the workload should be balanced throughout the execution, and the work scheduling/mapping should ensure matching of architectural features to algorithmic requirements.

In our effort to minimize communication, an example concerns the solution of general linear systems (via LU factorization) where the main objective is to reduce the communication overhead due to pivoting. We developed several algorithms to achieve this objective for hybrid CPU/GPU platforms. In one of them the panel factorization is performed using a communication-avoiding pivoting heuristic  [83] while the update of the trailing submatrix is performed by the GPU  [37] . In another algorithm, we use a random preconditioning (see also Section  3.2.2 ) of the original matrix to avoid pivoting  [40] . Performance comparisons and tests on accuracy showed that these solvers are effective on current hybrid multicore-GPU parallel machines. These hybrid solvers will be integrated in a next release of the MAGMA library.

Another issue is related to the impact of non-uniform memory accesses (NUMA) on the solution of HPC applications. For dense linear systems, we illustrated how an appropriate placement of the threads and memory on a NUMA architecture can improve the performance of the panel factorization and consequently accelerate the global LU factorization  [133] , when compared to the hybrid multicore/GPU LU algorithm as it is implemented in the public domain library MAGMA.

Research tracks for the 4 next years

Towards automatic generation of dense linear solvers:

In an ongoing research, we investigate a generic description of the linear system to be solved in order to exploit numerical and structural properties of matrices to get fast and accurate solutions with respect to a specific type of problem. Information about targeted architectures and resources available will be also taken into account so that the most appropriate routines are used or generated. An application of this generative approach is the possibility of prototyping new algorithms or new implementations of existing algorithms for various hardware.

A track for generating efficient code is to develop new functionalities in the C++ library $N{T}^2$  [75] which is developed in the Postale team. This approach will enable us to generate optimized code that support current processor facilities (OpenMP and TBB support for multicores, SIMD extensions...) and accelerators (GPU, Intel Xeon Phi) starting from an API (Application Programming Interface) similar to Matlab. By analyzing the properties of the linear algebra domain that can be extracted from numerical libraries and combining them with architectural features, we have started to apply the generic approach mentioned in Section  3.1.2 to solve dense linear systems on various architectures including CPU and GPU. As an application, we plan to develop a new software that can run either on CPU or GPU to solve least squares problems based on semi-normal equations in mixed precision  [36] since, to our knowledge, such a solver cannot be found in current public domain libraries (Sca)LAPACK  [29] , [54] , PLASMA  [150] and MAGMA  [38] . This solver aims at attaining a performance that corresponds to what state-of-the-art codes achieve using mixed precision algorithms.

Communication avoiding algorithms for heterogeneous platforms:

In previous work, we focused on the LU decomposition with respect to two directions that are numerical stability and communication issue. This research work has lead to the development of a new algorithm for the LU decomposition, referred to as LU_PRRP: LU with panel rank revealing pivoting  [98] . This algorithm uses a new pivoting strategy based on strong rank revealing QR factorization  [84] . We also design a communication avoiding version of LU_PRRP, referred to as CALU_PRRP, which aims at overcoming the communication bottleneck during the panel factorization if we consider a parallel version of LU_PRRP. Thus CALU_PRRP is asymptotically optimal in terms of both bandwidth and latency. Moreover, it is more stable than the communication avoiding LU factorization based on Gaussian elimination with partial pivoting in terms of growth factor upper bound  [64] .

Due to the huge number and the heterogeneity of computing units in future exascale platforms, it is crucial for numerical algorithms to exhibit more parallelism and pipelining. It is thus important to study the critical paths of these algorithms, the task decomposition and the task granularity as well as the scheduling techniques in order to take advantage of the potential of the available platforms. Our goal here is to adapt our new algorithm CALU_PRRP to be scalable and efficient on heterogeneous platforms making use of the available accelerators and coprocessors similarly to what was achieved in  [37] .

Application to numerical fluid mechanics:

In an ongoing PhD thesis  [153] , [154] , we apply hybrid programming techniques to develop a solver for the incompressible Navier-Stokes equations with constant coefficients, discretized by the finite difference method. In this application, we focus on solving large sparse linear systems coming from the discretization of Helmholtz and Poisson equations using direct methods that represent the major part of the computational time for solving the Navier-Stokes equations which describe a large class of fluid flows. In the future, our effort in the field will concern how to apply hybrid programming techniques to solvers based on iterative methods. A major task will consist of developing efficient kernels and choosing appropriate preconditioners. An important aspect is also the use of advanced scheduling techniques to minimize the number of synchronizations during the execution. The algorithms developed during this research activity will be validated on physical data provided by the physicists either form the academic world (e.g., LIMSI/University Paris-Sud (Laboratoire d'Informatique pour la Mécanique et les Sciences de l'Ingénieur, http://www.limsi.fr/ ) or industrial partners (e.g., EDF, ONERA). This research is currently performed in the framework of the CALIFHA project (CALculations of Incompressible Fluids on Heterogeneous, funded by Région Île-de-France and Digitéo (http://www.digiteo.fr )) and will be continued in an industrial contract with EDF R&D (starting October 2014).

Randomized algorithms in HPC applications

Activity description

Randomized algorithms are becoming very attractive in high-performance computing applications since they are able to outperform deterministic methods while still providing accurate results. Recent advances in the field include for instance random sampling algorithms  [33] , low-rank matrix approximation  [116] , or general matrix decompositions  [87] .

Our research in this domain consists of developing fast algorithms for linear algebra solvers which are at the heart of many HPC physical applications. In recent works, we designed randomized algorithms  [40] , [52] based on random butterfly transformations (RBT)  [121] that can be applied to accelerate the solution of general or symmetric indefinite (dense) linear systems for multicore  [35] or distributed architectures  [34] . These randomized solvers have the advantage of reducing the amount of communication in dense factorizations by removing completely the pivoting phase which inhibits performance in Gaussian Elimination.

We also studied methods and software to assess the numerical quality of the solution computed in HPC applications. The objective is to compute quantities that provide us with information about the numerical quality of the computed solution in an acceptable time, at least significantly cheaper than the cost for the solution itself (typically a statistical estimation should require $𝒪\left(n^2\right)$ flops while the solution of a linear system involves at least $𝒪\left(n^3\right)$ flops, where $n$ is the problem size). In particular, we recently applied in  [44] statistical techniques based on the small sample theory  [97] to estimate the condition number of linear system/linear least squares solvers  [31] , [39] , [43] . This approach reduces significantly the number of arithmetic operations in estimating condition numbers. Whether designing fast solvers or error analysis tools, our ultimate goal is to integrate the resulting software into HPC libraries so that these routines will be available for physicists. The targeted architectures are multicore systems possibly accelerated with GPUs or Intel Xeon Phi coprocessors.

This research activity benefits from the Inria associate-team program, through the associate-team R-LAS (Randomized Linear Algebra Software, https://www.lri.fr/~baboulin/presentation_r-las.html/ ), created in 2014 between Inria Saclay/Postale team and University of Tennessee (Innovative Computing Laboratory) in the area of randomized algorithms and software for numerical linear algebra. This project is funded from 2014 to 2016 and is lead jointly by Marc Baboulin (Inria/University Paris-Sud) and Jack Dongarra (University of Tennessee).

Research tracks for the 4 next years

Extension of random butterfly transformations to sparse matrices:

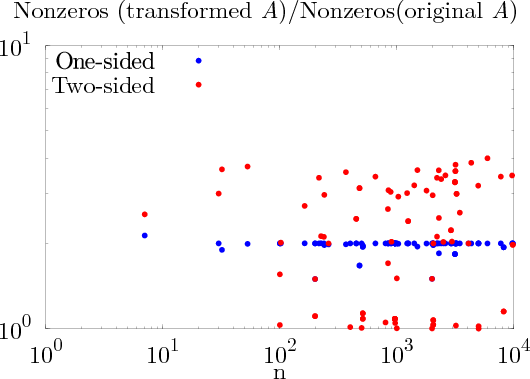
We recently illustrated how randomization via RBT can accelerate the solution of dense linear systems on multicore architectures possibly accelerated by GPUs. We recently started to extend this method to sparse linear systems arising from the discretization of partial differential equations in many physical applications. However, a major difficulty comes from the possible fill-in introduced by RBT. One of our first task consists of performing experiments on a collection of sparse matrices to evaluate the fill-in depending on the number of recursions in the algorithm. In a recent work  [45] , we investigated the possibility of using another form of RBT (one-side RBT instead of two-sided) in order to minimize the fill-in and we obtain promising preliminary results (Figure 4 shows that the fill-in is significantly reduced when using one-side RBT).

Another track of research is related to iterative methods for solving large sparse linear systems, and more particularly preconditioned Krylov subspace methods implemented in the solver ARMS (Algebraic Recursive Multilevel Solver (pARMS for its parallel distributed version). In this solver, our goal is to find the last level of preconditioning and then replace the original ILU factorization by our RBT preprocessing. A PhD thesis (supervised by Marc Baboulin) started in October 2014 on using randomization techniques like RBT for sparse linear systems.

Randomized algorithms on large clusters of multicore:

A major challenge for the randomized algorithms that we develop is to be able to solve very large problems arising in real-world physical simulations. As a matter of fact, large-scale linear algebra solvers from standard parallel distributed libraries like ScaLAPACK often suffer from expensive inter-node communication costs. An important requirement is to be able to schedule these algorithms dynamically on highly distributed and heterogeneous parallel systems  [96] . In particular we point out that even though randomizing linear systems removes the communication due to pivoting, applying recursive butterflies also requires communication, especially if we use multiple nodes to perform the randomization. Our objective is to minimize this communication in the tiled agorithms and to use a runtime that enforces a strict data locality scheduling strategy  [34] . A state of the art of possible runtime systems and how they can be combined with our randomized solvers will be established. Regarding the application of such solver, a collaboration with Pr Tetsuya Sakurai (University of Tsukuba, Japan) and Pr Jose Roman (Universitat Politècnica de València, Spain) will start in December 2014 to apply RBT to large linear systems encountered in contour integral eigensolver (CISS)  [94] . Optimal tuning of the code will be obtained using holistic approach developed in the Postale team  [79] .

Extension of statistical estimation techniques to eigenvalue and singular value problems:

The extension of statistical condition estimation techniques can be carried out for eigenvalue/singular value calculations associated with nonsymmetric and symmetric matrices arising in, for example, optimization problems. In all cases, numerical sensitivity of the model parameters is of utmost concern and will guide the choice of estimation techniques. The important class of componentwise relative perturbations can be easily handled for a general matrix  [97] . A significant outcome of the research will be the creation of high-quality open-source implementations of the algorithms developed in the project, similarly to the equivalent work for least squares problems  [41] . To maximize its dissemination and impact, the software will be designed to be extensible, portable, and customizable.

Random orthogonal matrices:

Random orthogonal matrices have a wide variety of applications. They are used in the generation of various kinds of random matrices and random matrix polynomials  [53] , [63] , [65] , [91] . They are also used in some finance and statistics applications. For example the random orthogonal matrix (ROM) simulation [113] method uses random orthogonal matrices to generate multivariate random samples with the same mean and covariance as an observed sample.

The natural distribution over the space of orthogonal matrices is the Haar distribution. One way to generate a random orthogonal matrix from the Haar distribution is to generate a random matrix $A$ with elements from the standard normal distribution and compute its QR factorization $A=QR$, where $R$ is chosen to have nonnegative diagonal elements; the orthogonal factor $Q$ is then the required matrix [90] .

Stewart [140] developed a more efficient algorithm that directly generates an $n\times n$ orthogonal matrix from the Haar distribution as a product of Householder transformations built from Householder vectors of dimensions $1,2,\cdots ,n-1$ chosen from the standard normal distribution. Our objective is to design an algorithm that significantly reduces the computational cost of Stewart's algorithm by relaxing the property that $Q$ is exactly Haar distributed. We also aim at extending the use of random orthogonal matrices to other randomized algorithms.

Embedded high-performance systems & computer vision

Scientific context

High-performance embedded systems & computer vision address the design of efficient algorithms for parallel architectures that deal with image processing and computer vision. Such systems must enforce realtime execution constraint (typically 25 frames per second) and power consumption constraint. If no COTS (Component On The Shelf) architecture (e.g., SIMD multicore processor, GPU, Intel Xeon Phi, DSP) satisfy the constraints, then we have to develop a specialized one.

A more and more important aspect when designing an embedded system is the tradeoff between speed (and power consumption) and numerical accuracy (and stability). Such a tradeoff leads to 16-bit computation (and storage) and to the design of less accurate algorithms. For example, the final accuracy for stabilizing an image is $10-1$ pixel, which is far from the maximum accuracy of (${10}^{-7}$) available using the 32-bit IEEE format.

Activity description and recent achievements

Concerning image processing, our efforts concern the redesign of data-dependent algorithms for parallel architectures. A representative example of such an algorithm is the connected-component labeling (CCL) algorithm  [132] which is used in industrial or medical imaging and classical computer vision like optical character recognition. As far as we know our algorithm (Light Speed Labeling)  [57] , [58] still outperforms other existing CCL algorithms  [82] , [89] , [145] (the first versions of our algorithm appeared in 2009  [105] , [106] ).

Concerning computer vision (smart camera, autonomous robot, aerial drone), we developed in collaboration with LIMSI (Laboratoire d'Informatique pour la Mécanique et les Sciences de l'Ingénieur) two applications that run in realtime on embedded parallel systems [107] , [131] with some accuracy tradeoffs. The first one is based on mean shift tracking [80] , [81] and the second one relies on covariance matching and tracking [128] , [129] , [130] .

These applications are used in video-surveillance: they perform motion detection  [104] , motion analysis  [146] , [147] , motion estimation and multi-target tracking. Depending on the image nature and size, some algorithmic transforms (integral image, cumulative differential sum) can be applied and combined with hybrid arithmetic (16-bit / 32-bit / 64-bit). Finally, to increase the algorithm robustness color, space optimization is also used [108] .

Usually one tries to convert 64-bit computations into 32-bit. But sometimes 16-bit floating point arithmetic is sufficient. As 16-bit numbers are now normalized by IEEE (754-2008) and are available in COTS processors like GPU and GPP (AVX2 for storage in memory and conversion into 32-bit numbers), we can run such kind of code on COTS processors or we can design specialized architectures like FPGA (Field-Programmable gate array) and ASIC (Application-specific integrated circuit) to be more efficient. This approach is complementary to that of  [117] which converts 32-bit floating point signal processing operators into fixed-point ones.

By extension to computer vision, we also address interactive sensing HPC applications. One CEA thesis funded by CEA and co-supervised by Lionel Lacassagne addresses the parallelization of Non Destructive Testing applications on COTS processors (super-charged workstation with GPUs and Intel Xeon Phi manycore processor). This PhD thesis deals with irregular computations with sparse-addressing and load-balacing problems. It also deals with floating point accuracy, by finding roots of polynomials using Newton and Laguerre algorithms. Depending on the configuration, 64-bit is required, but sometime 32-bit computations are sufficient with respect to the physics. As the second application focuses on interactive sensing, one has to add a second level of tradeoff for physical sampling accuracy and the sensor displacement [109] , [110] , [111] , [126] , [127] .

In order to achieve realtime execution on the targeted architectures, we develop High Level Transforms (HLT) that are algorithmic transforms for memory layout and function re-organization. We show on a representative algorithm [88] in the image processing area that a fully parallelized code (SIMD+OpenMP) can be accelerated by a factor $\times 80$ on a multicore processor  [101] . A CIFRE thesis (defended in 2014) funded by ST Microelectronics and supervised by Lionel Lacassagne has led to the design of very efficient implementations into an ASIC thanks to HLT. We show that the power consumption can be reduced by a factor 10 [155] , [156] .

All these applications have led to the development of software libraries for image processing that are currently under registration at APP (Agence de Protection des Programmes): myNRC 2.0 (smart memory allocator and management for 2D and 3D image processing) and covTrack (agile realtime multi-target tracking algorithm, co-developped with Michèle Gouiffès at LIMSI).

Future: system, image & arithmetic

Concerning image processing we are designing new versions of CCL algorithms. One version is for parallel architectures where graph merging and efficient transitive closure is a major issue for load balancing. For embedded systems, time prediction is as important as execution time, so a specialized version targets embedded processors like ARM processors and Texas Instrument VLIW DSP C6x.

We also plan to design algorithms that should be less data-sensitive (the execution time depends on the nature of the image: a structured image can be processed quickly whereas an unstructured image will require more time). These algorithms will be used in even more data-dependent algorithms like hysteresis thresholding for image binarization, split-and-merge [30] , [100] for realtime image segmentation using the Horowitz-Pavlidis quad-tree decomposition [93] . Such an algorithm could be useful for accelerating image decomposition like Fast Level Set Transform algorithm [118] .

Concerning Computer vision we will study 16-bit floating point arithmetic for image processing applications and linear algebra operators. Concerning image processing, we will focus on iterative algorithms like optical flow computation (for motion estimation and image stabilization). We will compare the efficiency (accuracy and speed) of 16-bit floating point [72] , [103] , [102] , [124] with fixed-point arithmetic. Concerning linear algebra, we will study efficient implementation for very small matrix inversion (from $6\times 6$ up to $16\times 16$) for our covariance-tracking algorithm.

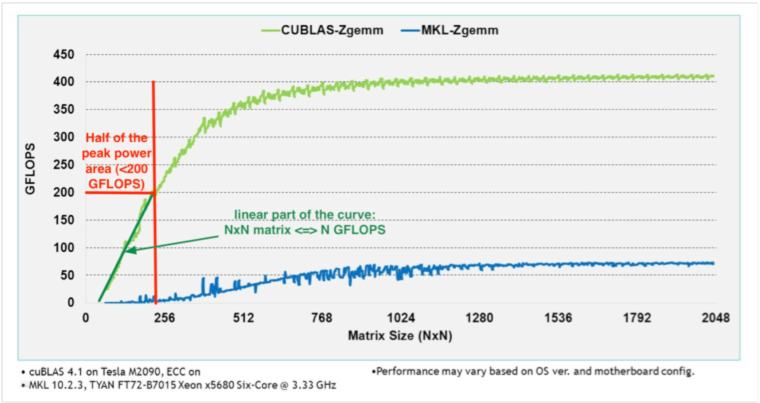
According to Nvidia (see Figure 5 ), the computation rate (Gflop/s) for ZGEMM (complex matrix-matrix multiplication with 64-bit precision – for small value of $N$ – is linearly proportional to $N$. That means that, for a $6\times 6$ matrix, we achieve around 6 Gflop/s on a Tesla M2090 (400 Gflop/s peak power). This represents 1.5 % of the peak power. For that reason, designing efficient parallel codes for embedded systems [60] , [67] , [68] is different and may be more complex than designing codes for classical HPC systems. Our covTrack software requires many hundreds of $6\times 6$ matrix-matrix multiplications every frame.

Last point is to develop tools that help to automatically distribute or parallelize a code on an architecture code parallelization/distribution dealing with scientific computing [69] , MPI [73] or image applications on the Cell processor [61] , [74] , [123] , [134] , [135] , [136] , [148] .